Friday, December 26th, 2014
Compression is the process of reducing the storage space requirement for a set of data by converting it
into a more compact form than its original format. This concept of data compression is fairly old, dating at least
as far back as the mid 19th century, with the invention of Morse Code.
Morse Code was created to enable operators to transmit textual messages across an electrical telegraph system using a
sequence of audible pulses to convey characters of the alphabet. The inventors of the code recognized that
some letters of the alphabet are used more frequently than others (e.g. E is much more common than X), and therefore
decided to use shorter pulse sequences for more common characters and longer sequences for less common ones. This
basic compression scheme provided a dramatic improvement to the system's overall efficiency because it enabled operators to
transmit a greater number of messages in a much shorter span of time.
Although modern compression processes are significantly more complicated than Morse Code, they still rely on the same
basic set of concepts, which we will review in this article. These concepts are essential to the efficient operation
of our modern computerized world — everything from local and cloud storage to data streaming over the Internet relies heavily
on compression and would likely be cost ineffective without it.
Compression Pipeline
The following figure depicts the general paradigm of a compression scheme. Raw input data consists of a sequence of symbols that we wish to compress, or reduce in size. These symbols are encoded by the compressor, and the result is coded data. Note that although the coded data is usually smaller than the raw input data, this is not always the case (as we'll see later).

Coded data may then be fed into a decompressor, usually at a later point in time, where
it is decoded and reconstructed back into raw data in the form of an output sequence of symbols.
Note that throughout this article we'll use the terms sequence and string interchangably to refer to a
sequential set of symbols.
If the output data is always identical to the input, then the compression scheme is said to be
lossless, and utilizes a lossless encoder. Otherwise, it is a lossy compression scheme.
Lossless compression schemes are usually employed for compression of text, executable programs,
or any other type of content where identical reconstruction is required. Lossy compression schemes
are useful for images, audio, video, or any content where some degree of information loss is acceptable in
order to gain improved compression efficiency.
Data Modelling
Information is defined as a quantity that measures the complexity of a piece of data. The more information
that a data set has, the harder it is to compress it. The notion of rarity is correlated with this concept of
information because the occurrence of a rare symbol provides more information than the occurrence of a
common one.
For example, the occurrence of an earthquake in Japan would provide less information than an earthquake
on the moon, as earthquakes are far less common on the moon. We can expect most compression algorithms to
carefully regard the frequency or probability of a symbol when deciding how to compress it.
We describe the efficiency of a compression algorithm as its effectiveness at reducing information load.
A more efficient compression algorithm will reduce the size of a particular data set more than a less efficient algorithm.
Probability Models
One of the most important steps in designing a compression scheme is to create a probability model for the data. This model allows us to examine the characteristics of the data in order to efficiently fit a compression algorithm to it. Let's walk through part of the modelling process to make this a bit more clear.
Let's assume we have an alphabet, G, which consists of all possible symbols in a data set. In our example, G contains precisely four symbols: A through D.
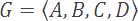
We also have a probability density function, P, which defines the probabilities for each symbol in G actually occurring in an input string. Symbols with higher probabilities are more likely to occur in an input string than symbols with lower probabilities.
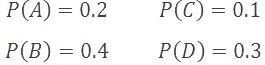
For this example we will assume that our symbols are independent and identically distributed. The presence of one symbol in a source string is expected to have no correlation to the presence of any other.
Minimum Coding Rate
B is our most common symbol, with a probability of 40%, while C is our least likely symbol, which occurs only 10% of the time. Our goal will be to devise a compression scheme that minimizes the required storage space for our common symbols, while supporting an increase in the necessary storage space for more rare symbols. This trade off is a fundamental principle of compression, and inherint in virtually all compression algorithms.
Armed with the alphabet and pdf, we can take an initial shot at defining a basic compression scheme. If we simply encoded
symbols as raw 8 bit ASCII values, then our compression efficiency, known as the coding rate, would be 8 bits per symbol.
Suppose we improve this scheme by recognizing that our alphabet contains only 4 symbols. If we dedicate 2 bits for each symbol,
we will still be able to fully reconstruct a coded string, but require only 1/4th the amount of space.
At this point we have significantly improved our coding rate (from 8 to 2 bits per symbol), but have completely ignored our probability model.
As previously suggested, we can likely improve our coding efficiency by incorporating our model, and devising a strategy that
dedicates fewer bits to the more common symbols (B and D), and more bits to the less common symbols (A and C).
This brings up an important insight first described in Shannon's seminal paper
— we can define the theoretical minimum required storage space for a symbol (or event) based simply on its probability.
We define the minimum coding rate for a symbol as follows:
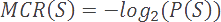
For example, if a symbol occurs 50% of the time, then it would require, at an absolute minimum, 1 bit to store it.
Entropy and Redundancy
Going further, if we compute a weighted average of the minimum coding rates for the symbols in our alphabet, we arrive at a value that is known as the Shannon entropy, or simply the entropy of the model. Entropy is defined as the minimum coding rate at which a given model may be coded. It is based on an alphabet and its probability model, as described below.
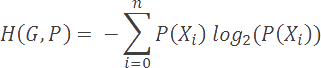
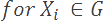
As one might expect, models with many rare symbols will have a higher entropy than models with fewer and more common symbols. Furthermore, models with higher entropy values will be harder to compress than those with lower entropy values.
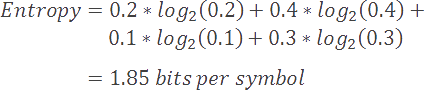
In our current example, our model has an entropy of 1.85 bits per symbol. The difference between our current coding rate (2) and entropy (1.85) is known as the redundancy of our compression scheme.
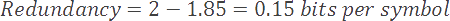
Entropy is an extremely useful topic with applicability to many different subfields including encryption and artificial
intelligence. A full discussion of entropy is outside the scope of this article, but interested readers can learn much more
here.
Coding the Model
We've taken a slight liberty thus far, and have automatically given ourselves the probabilities of our symbols. In reality, the model may not always be readily available and we will need to derive these values either through analysis of source strings (e.g. by tallying symbol probabilities from exemplar data), or by adaptively learning the model in tandem with a compression process. In either case, the probabilities of the actual source data may not perfectly match the model, and we will lose efficiency proportional to this divergence. For this reason, it is important to derive (or constantly maintain) as accurate a model as possible.
Common Algorithms
Once the probability model is defined for a set of data, we are able to devise a compression scheme that properly leverages
the model. While the process of developing a new compression algorithm is beyond the scope of this article, we can leverage
existing algorithms to fit our needs. We review some of the most popular algorithms below.
Each of the following algorithms is a sequential processor, which means that in order to reconstruct the nth element
from a coded sequence, the previous 0...(n-1) symbols must first be decoded. Seeking operations are not possible because
of the variable length nature of the encoded data — the decoder has no way of jumping to the correct offset for symbol n
without first decoding all previous symbols. Additionally, some coding schemes rely on internal historical state that is maintained only
by processing each symbol within a sequence in order.
Huffman Coding
This is one of the most well known compression schemes and it dates back to the early 1950s, when David Huffman
first described it in his paper,
"A Method for the Construction of Minimum Redundancy Codes." Huffman coding
works by deriving an optimal prefix code for a given alphabet.
A prefix code ascribes a numerical value to each symbol in an alphabet such that no symbol's code is a prefix for
any other symbol's code. For example, if 0 is the code for our first symbol, A, then no other symbol in our alphabet
may begin with a 0. Prefix codes are useful because they enable precise and unambiguous decoding of a bit stream.
The process for deriving an optimal prefix code for a given alphabet (the essence of Huffman coding) is outside the scope of this article, but check out my other blog post that describes the process in detail.
The following table illustrates the Huffman codes for all symbols in our alphabet.

Now, let's examine the effectiveness of a sample prefix code for our example alphabet, G. Notice that we've assigned shorter codes to more common symbols, and longer codes to less common ones.
Using this system, our average coding rate is significantly reduced to 1.9 bits per symbol, versus our previous best value of 2, and our redundancy is reduced to 0.05 bits per symbol (versus 0.15).
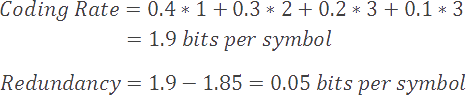
Dictionary Approaches
Coders of this type leverage a dictionary to store recently observed symbols. When a
symbol is encountered, it is first checked against the dictionary, to see if it is already
stored. If it is, then the output will simply consist of a reference to the dictionary entry
(usually an offset), rather than the full symbol.
Examples of common dictionary based compression schemes include LZ77 and LZ78, which
serve as the foundation for many different lossless encoding schemes.
In some cases, a sliding window is used to adaptively track recently seen symbols. In these cases,
a symbol is only maintained in the dictionary if it has been seen relatively recently. Otherwise,
the symbol is evicted (and potentially re-entered for a later occurrence). This process prevents
symbol indices from growing too large, and leverages the fact that symbols in a sequence may
recur within a relatively short window.
Exponential Golomb Coding
Imagine you have an alphabet consisting of integers within the range of 0 to 255, and that the probability
for a symbol is related to its distance from zero. In this case, low values are the most common, and higher values are increasingly more rare.
For this scenario, an Exponential Golomb Coder might be useful. Golomb coding uses a specific prefix code
that gives preference to low values at the expense of high values. The following table illustrates the
first few values:

The process for encoding an integer is straightforward. First, increment the integer value and count the number
of bits required to store this new value. Next, subtract one from the bit count and output this number of zeroes to
the output stream. Lastly, output the incremented value (computed in the first step) to the bit stream.
For example, a value of 4 would be incremented to 5, or 101 binary. This value requires 3 bits for storage, so we
output 2 zeroes to the output stream, followed by our binary value of 101. The result is 00101.
Like most compression schemes, the effectiveness of Golomb coding is heavily dependent upon the specific symbols in the
source sequence. Sequences containing many high values will compress much more poorly than sequences with fewer, and in
some cases, a Golomb coded sequence may even be greater in size than the original input string.
For more information about this coding scheme, check out this project.
Arithmetic Coding
Arithmetic coding is a novel compression algorithm that has recently (within the last 15 years) gained
tremendous popularity, particularly for media compression. Arithmetic coders are highly efficient, computationally
intensive and sequential in nature.
A common variant of arithmetic coding, called binary arithmetic coding, uses
only two symbols (0 and 1) in its alphabet. This variation is particularly useful because it simplifies the
design of the coder, lowers the runtime computational costs, and does not require any explicit communication
between the compressor and decompressor to communicate an alphabet and model.
For more information about arithmetic coding, check out my other article, Context Adaptive Binary
Arithmetic Coding.
Run Length Encoding (RLE)
Thus far we've assumed that our source symbols are independent and identically distributed. Our
probability model and measurements for coding rate and entropy have relied upon this fact, but what
if our sequence of symbols does not satisfy this requirement?
Suppose that repetition is very likely within our sequence, and that the presence of one particular
symbol strongly suggests that repeated instances of it will follow. In this case, we may choose to
use another encoding scheme known as run length encoding. This technique performs well with highly
repetitive symbols, and poorly when there is little repetition.
Run length encoders anticipate stretches of repeated symbols within a string, and replace
them with a pair consisting of a copy of the symbol followed by a repetition count.
For example, the sequence AABBBBBBBDDD contains repetitions of A, B, and D, and would
be run length encoded as the sequence A2B7D3 to represent the fact that A is repeated twice, B seven times,
and D three times. Upon reconstruction, the decoder will repeat each letter according to
the repetition count specified in the string to arrive back at the original input string.
As we've previously mentioned, this algorithm is suitable for strings with high repetition, but
notice what happens when encoding a string with minimal repetition: ABCDABCD becomes A1B1C1D1A1B1C1D1, which
is far worse than the original source. Similar to most other compression algorithms, the efficiency of run
length encoding is heavily dependent upon how well the source string matches the underlying model of the
algorithm. In the most severe cases, run length encoding may produce a compressed result that is 2 times
larger than the source input.
A Lossy Note
Although lossy compression is outside the scope of this article, it is important to note that lossy compression often utilizes a lossless compressor as a part of its pipeline. Lossy compression may be achieved as a two step process where data is first carefully decimated (to discard unwanted or unnecessary information), and then compressed using a lossless algorithm. Popular image and video codecs such as JPEG and H.264 do precisely this, and rely upon lossless algorithms such as Huffman encoding or arithmetic encoding to help achieve their great efficiencies.
Conclusion
This article has focused on lossless compression techniques and provided a brief introduction to some of the most popular techniques. Hopefully this has piqued your interest in the important field of data compression, and provided pointers for further reading on the subject.