Saturday, April 18th, 2015
Denoising is a very useful process that's used in video compression, computer vision, video capture pipelines, and more.
Anywhere that noise may find its way into an image, denoising filters are there to help clean things up. There are many
different kinds of noise, and fortunately there are equally many ways of correcting it.
Modern video codecs include denoising filters to mitigate some of the artifacts produced by the encoding process.
The Cairo codec is no exception, and uses a simple denoise filter during
image decoding to smooth out noise that may find its way into a frame.
As mentioned, there are many different kinds of noise, but I'd like
to focus this article on one particular type: salt and pepper noise. This kind of noise presents as speckled light and dark
pixels that can give a frame a grainy look and degrade the clarity of the image. Sometimes these artifacts are desirable,
as they can mimic film grain or other visual qualities, but when they are introduced by the codec, it's best to rectify them.
Let's say we have the following image that exhibits significant noise:

Removing this kind of noise is a simple process:
First we convert our rgb input image into the yuv color space. This allows us to separate the brightness (luma) from the color (chroma) of the frame.
Next we divide the luma image into symmetric blocks of pixels known as macroblocks. These blocks may vary in size, but in the case of the Cairo codec (and many others, including JPEG), they are always 8x8 pixels in dimension.
For each macroblock in our luma image we perform a discrete cosine transform to convert our spatial pixel data into the frequency domain. Each 8x8 block of color values is replaced by an 8x8 block of frequency coefficients.
These blocks exhibit a special pattern: the upper left coefficient corresponds to the lowest frequency in the block, while the lower right coefficient corresponds to the highest frequency in the block.
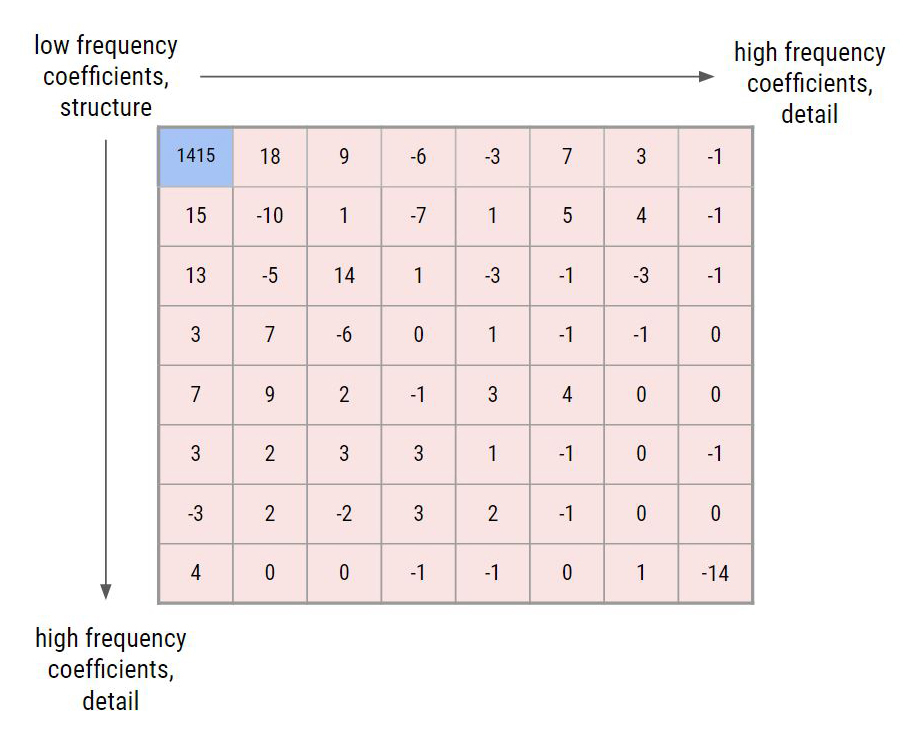
Thus, as we move to the right and down the block, we access coefficients of increasing frequencies. This is notable because lower frequency coefficients represent the structure of an image, while higher frequency coefficients represent the detail – and it is within this detail that we find our noise. Salt and pepper noise represents very high frequency data, so it will predominantly affect our lower right-hand range of each transformed coefficient block.
Our next step is to decide how to isolate the noisy coefficients. Cairo uses a sophisticated set of heuristics but the work can be summarized as figuring out which high frequency coefficients need to be adjusted, and by how much. This usually involves analyzing and blending across high frequency coefficients within neighboring blocks. The result should preserve high frequency coefficients when they accurately represent detail, and reduce them when they represent noise.
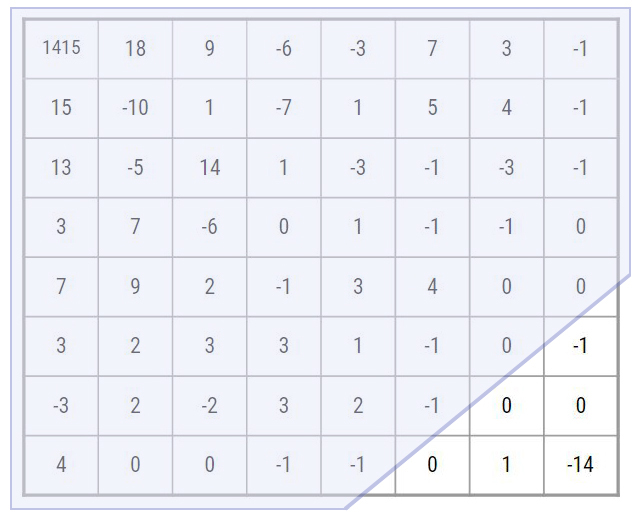
For the purposes of this article let's simply assume that the lower right 1/16th of the block should be filtered. We perform a simple low pass filter to that preserves our low frequency coefficients (outlined in light purple above) and zeroes out our high frequency ones (lower right unshaded region). This results in the following block:
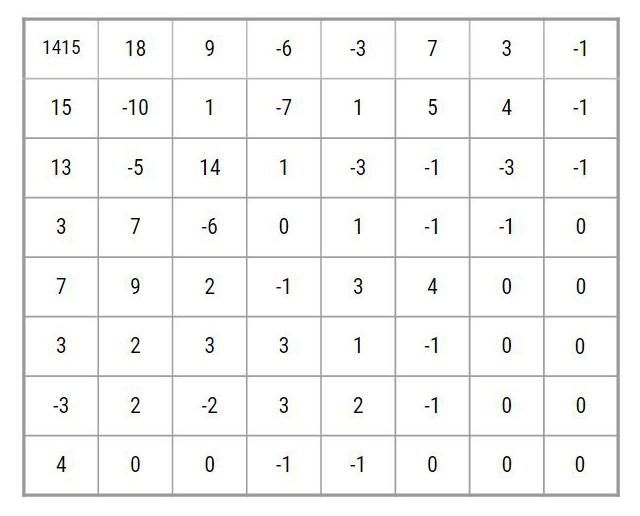
We perform these steps for all macroblocks in our luma image, and repeat them for all blocks in our chroma images. Once complete, we perform an inverse transform on our blocks in order to reconstruct the filtered pixel values. We may also choose to perform heavier denoising on the luma image than on the chroma images, as humans are more sensitive to changes in brightness (and noise), than they are to changes in color. Our final result is the following:

This is an improvement over our original image, but the image continues to exhibit significant noise. To clean this up further Cairo employs more sophisticated filtering of high frequency coefficients, and bilinear interpolation of pixel values to smooth out abrupt changes in the data. Once we apply these practices the image improves considerably:

The final result displays far fewer artifacts for a much clearer image. The image below shows a closer comparison of the before and after.

We've discussed a very simple process for reducing salt and pepper noise in an image. This process yields surprisingly good results because we've focused our
problem on a very particular type of high frequency noise.
In practice, effective denoise filters must be highly adaptive in order to cope with the broad array of artifacts that may be
encountered, and the key is finding the right balance between noise reduction, detail preservation, and computational cost.
For more information about Cairo's denoise filter, check out its source code at this github repo.